|
16:46
классическое определение вероятности события
|
|
Задача. Из 60 вопросов, входящих в экзаменационные билеты, студент подготовил 50. Какова вероятность того, что взятый наудачу студентом билет, содержащий 2 вопроса, будет состоять из подготовленных им вопросов?
РЕШЕНИЕ
1) Обозначим событие А = «Вытянутый студентом билет состоит из подготовленных им билетов». Для вычисления вероятности появления данного события воспользуемся классическим определением вероятности события, согласно которому вероятность определяется по формуле: 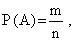 где m – число исходов, при которых появляется событие А, n – общее число элементарных несовместных равновозможных исходов. 2) Определим n. Общее число билетов определяется сочетанием по 2 из 60: 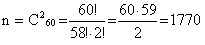 3) Количество билетов, вопросы которых студент знает, определяется сочетанием по 2 из 50: 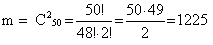 4) Определим вероятность события А: 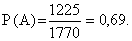 ОТВЕТ: Вероятность того, что взятый наудачу студентом билет, содержащий 2 вопроса, будет состоять из подготовленных им вопросов равна Р(А) = 0,69. То есть, если будет, например, 100 таких студентов, то 69 из них вытянут билеты, к вопросам которых они подготовлены. Онлайн сервис: решение задач по теории вероятности |
|
|
| Всего комментариев: 0 | |
