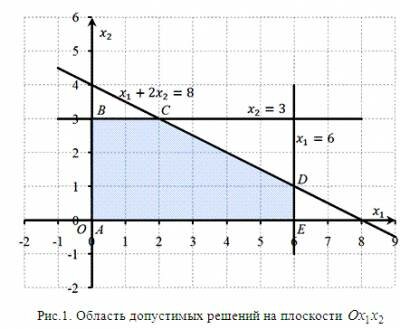
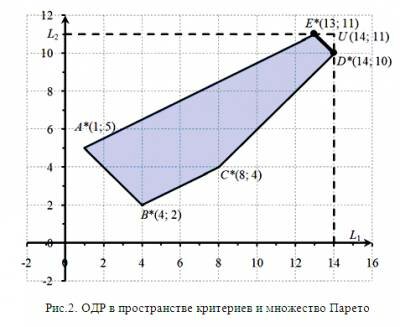
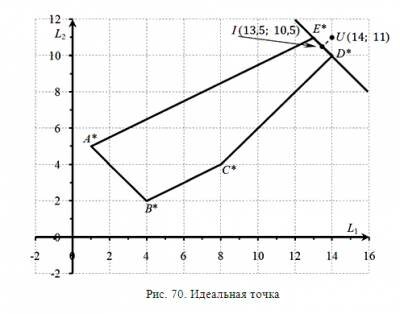
Методы решения многокритериальных задач

Метод идеальной точки

Задача линейной многокритериальной максимизации с двумя переменными и двумя целевыми функциями

Пример 1. Найти значения переменных, при которых функции

L₁ = 2x₁ + x₂ + 1 → max

L₂ = x₁ - x₂ + 5 → max

при ограничениях:

x₁ + 2x₂ ≤ 8,

0 ≤ x ≤ 6,

0 ≤ x ≤ 3.

Решение.

1) Построим область допустимых решений. Введем на плоскости прямоугольную систему координат  и построим множество X  — область допустимых решений данной задачи в указанной системе координат. Ограничительные условия определяют на плоскости многоугольник ABCDE (Рис. 1), вершины которого имеют соответственно координаты: (0; 0), (0; 3), (2; 3), (6; 1), (6; 0). Следовательно,  представляет собою многоугольник ABCDE.

2) Строим область допустимых решений в пространстве критериев. Подвергнем координаты каждой точки плоскости  преобразованиям L₁ = 2x₁+x₂+1 → max  и  L₂ = x₁-x₂+5 → max . Получим плоскость OL₁L₂. При этом в силу линейности проводимых преобразований прямоугольная система координат  перейдет в прямоугольную систему координат , а многоугольник ABCDE в многоугольник A*B*C*D*E*, вершины которого имеют соответственно координаты: (1; 5), (4; 2), (8; 4), (14; 10), (13; 11) (рис. 2).

 Для наглядности укажем описанное соответствие вершин: A(0; 0) → A*(1; 5), B(0; 3) → B*(4; 2), C(2; 3) → C*(8; 4), D(6; 1) → D*(14; 10), E(6; 0) → E*(13; 11).

Таким образом, все точки, координаты которых удовлетворяют условиям L₁ = 2x₁+x₂+1 → max,  L₂ = x₁-x₂+5 → max  и  (x₁, x₂) ϵ X, определяют на плоскости многоугольник A*B*C*D*E*. Следовательно, область допустимых решений  данной задачи в системе координат (пространстве критериев) представляет собою многоугольник A*B*C*D*E*.

3) Находим множество Парето. Это отрезок D*E*.

4) Находим точку утопии. Выбираем комбинацию наилучших значений всех критериев. В данном случае это точка U с координатами (14; 11).

5) Находим идеальную точку. Теперь необходимо найти во множестве Парето точку, расположенную ближе всех к точке утопии U. Из рис. 2 видно, что точка I( I₁, I₂ ), являющаяся основанием перпендикуляра, проведенного из точки U (14; 11) к прямой D*E*, принадлежит отрезку D*E*. Это означает, что точка I — искомая.

6) Находим  координаты идеальной точки. Сейчас необходимо вспомнить аналитическую геометрию: находим уравнение прямой D*E* и находим точку пересечения перпендикуляра проходящего через точку утопии U получаем координаты идеальной точки I( I₁, I₂ ).

Замечание. При нахождении расстояния между точкой утопии и идеальной точкой, учитывая топологию множества Парето, был применен «геометрический» метод. В общем случае задача нахождения расстояния между указанными точками решается как экстремальная. Необходимо найти на множестве Парето точку, такую, что расстояние между ней и точкой утопии минимально: