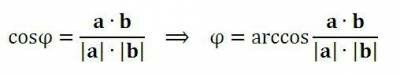Скалярное произведение векторов

Формулы, примеры, калькулятор скалярного произведения, а также угла между векторами.

Геометрическое определение. Скалярным произведением двух векторов a и b называется ЧИСЛО, равное произведению длин этих векторов на косинус угла φ между ними:

a • b = |a|•|b|cosφ

Угол между векторами

находим по формуле

Аналитическое определение скалярного произведения в координатах.

Формулы скалярного произведения векторов заданных координатами

На плоскости:  координаты векторов  a=(a_x,a_y), b=(b_x,b_y)

a • b = a_x • b_x+ a_y • b_y

В пространстве:  

координаты векторов  a=(a_x,a_y,a_z), b=(b_x,b_y,b_z)

a • b = a_x • b_x + a_y • b_y + a_z • b_z

Пример 1. Найти скалярное произведение векторов заданных координатами  a=(5,7,8), b=(4,-2,6)

Решение. По формуле скалярного произведения в пространстве, получаем

a • b = (5,7,8)•(4,-2,6) = 5•4+7•(-2)+8•6 = 54

Проверить правильность решения, можно с помощью калькулятора скалярного произведения (калькулятор универсальный, вычисляет скалярное произведение на плоскости, в пространстве, а также в пространстве n измерений).

Пример 2. Найти скалярное произведение векторов a и b, если их длины |a| = 3, |b| = 6, а угол между векторами равен 60˚.

Решение. Скалярное произведение находим по формуле

a • b = |a|•|b|cosφ = 3•6•cos 60 = 9

Решение с помощью калькулятора.

Пример 3. Найти угол между векторами заданными координатами  a=(5,7,8), b=(4,-2,6)

Решение. По формуле скалярного произведения в пространстве, получаем

Свойства скалярного произведения векторов

1. Скалярное произведение вектора самого на себя всегда больше или равно нуля:   a • a ≥ 0
2. Скалярное произведение вектора самого на себя равно нулю тогда и только тогда, когда вектор равен нулевому вектору:  a • a = 0 <=> a=0
3. Скалярное произведение вектора самого на себя равно квадрату его модуля: a • a =|a|²
4. Операция скалярного умножения коммуникативна :     a • b = b • a
5. Если скалярное произведение двух не нулевых векторов равно нулю, то эти вектора ортогональны:     a ≠ 0, b ≠ 0,  <=>  a⊥b
6. Операция скалярного умножения дистрибутивна:

(a + b) • c = a • c + b • c