Найти точки разрыва функции, если они существуют. Сделать чертеж.
Классификация точек разрыва функции
Все точки разрыва функции разделяются на точки разрыва первого и второго рода.Говорят, что функция
- Существуют левосторонний предел
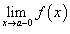 и правосторонний предел
и правосторонний предел 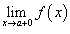 ;
; - Эти односторонние пределы конечны.
- Левосторонний предел и правосторонний предел равны друг другу:
Такая точка называется точкой устранимого разрыва.
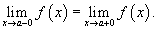
- Левосторонний предел и правосторонний предел не равны друг другу:
Такая точка называется точкой конечного разрыва. Модуль разности значений односторонних пределов
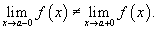
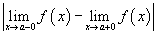 называется скачком функции.
называется скачком функции.
По данной теме также смотрят: калькулятор точек разрыва
| 16.11.2012, 13:39 | ||||||||||||||||
Задание на картинке
|
||||||||||||||||
 |
 |
|
|
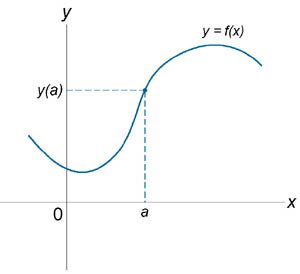
Непрерывна при
|
Имеет разрыв при
|
|
 |
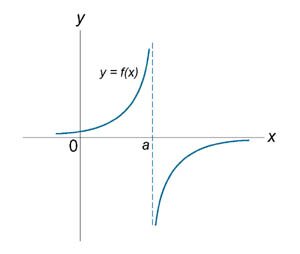 |
|
|
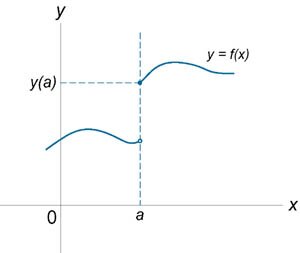
Непрерывна при
|
Имеет разрыв при
|
|
|
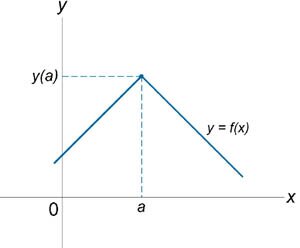
Рисунок 1.
|
||
| Всего комментариев: 0 | |

