Синтаксис Wolfram Alpha

Меню сайта

Новые материалы

Планом торговой фирмы «М-Аудио» на предстоящий период предусматривалось увеличение розничного товарооборота

Решить рекуррентное соотношение методом производящих функций

формула включений и исключений для трех множеств

Комбинаторные уравнения

Специальная математика

Случай - что это

Однородный шар катится без скольжения вверх по наклонной плоскости

Пространство элементарных событий

алгебра событий

Формула Бернулли задачи

Статистика

Онлайн всего: 39

Гостей: 39

Пользователей: 0

Контрольные

Заказать решение в авторском исполнении

Сейчас смотрят

Как найти площадь фигуры ограниченной линиями онла...

Калькулятор для исследования функций

Решение тригонометрических уравнений онлайн

Решение логарифмических уравнений онлайн

Найти экстремум функции

Калькулятор решения пределов

Решение дифференциальных уравнений онлайн

Изменить порядок интегрирования в двойном интеграл...

Решение двойных интегралов онлайн

Найти частные производные

калькулятор сходимости рядов

скнф и сднф

решение показательных уравнений

Как правильно вводить формулы на вольфрам альфа

Основные операции

Сложение $a+b$ : a+b
Вычитание $a-b$ : a-b
Умножение $a\cdot b$ : a*b
Деление $\frac{a}{b}$ : a/b
Возведение в степень 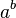${{a}^{b}}$ : a^b

Примеры

314+278; 314—278; 314*278; 314^278;
(a^2+b^2)+(a^2-b^2); (a^2+b^2)/(a^2-b^2); (a+b)^(2+2/3).

Знаки сравнения

Меньше $<$ : <
Больше $>$ : >
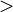Равно $=$ : = или ==
Меньше или равно $\le$ : <=
Больше или равно $\ge$ : >=

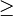Логические символы

И $\wedge$ : &&
ИЛИ $\vee$ : ||
НЕ $\neg$ : !

Основные константы

Число $\pi$ : Pi
Число $e$ : E
Бесконечность $\infty$ : Infinity или inf

Основные функции

$\left(a=\operatorname{const} \right)$

$x^{a}$ : x^a

модуль x: abs(x)

$\sqrt{x}$ : Sqrt[x]
$\sqrt[n]{x}$ : x^(1/n)
$a^{x}$ : a^x
$\log_{a}x$ : Log[a, x]
$\ln x$ : Log[x]
$\cos x$ : cos[x] или Cos[x]
$\sin x$ : sin[x] или Sin[x]
$\operatorname{tg}x$ : tan[x] или Tan[x]
$\operatorname{ctg}x$ : cot[x] или Cot[x]
$\sec x$ : sec[x] или Sec[x]
$\operatorname{cosec} x$ : csc[x] или Csc[x]
$\arccos x$ : ArcCos[x]
$\arcsin x$ : ArcSin[x]
$\operatorname{arctg} x$ : ArcTan[x]
$\operatorname{arcctg} x$ : ArcCot[x]
$\operatorname{arcsec} x$ : ArcSec[x]
$\operatorname{arccosec} x$ : ArcCsc[x]
$\operatorname{ch} x$ : cosh[x] или Cosh[x]
$\operatorname{sh} x$ : sinh[x] или Sinh[x]
$\operatorname{th} x$ : tanh[x] или Tanh[x]
$\operatorname{cth} x$ : coth[x] или Coth[x]
$\operatorname{sech} x$ : sech[x] или Sech[x]
$\operatorname{cosech} x$ : csch[x] или Csch[е]
$\operatorname{areach} x$ : ArcCosh[x]
$\operatorname{areash} x$ : ArcSinh[x]
$\operatorname{areath} x$ : ArcTanh[x]
$\operatorname{areacth} x$ : ArcCoth[x]
$\operatorname{areasech} x$ : ArcSech[x]
$\operatorname{areacosech} x$ : ArcCsch[x]
[19.67] =19: integral part of (19.67) - выделяет целую часть числа (integerPart)

Решение уравнений

Чтобы получить решение уравнения вида $f(x)=0$ достаточно записать в строке Wolfram|Alpha: f[x]=0, при этом Вы получите некоторую дополнительную информацию, которая генерируется автоматически. Если же Вам необходимо только решение, то необходимо ввести: Solve[f[x]=0, x].

Примеры

Solve[Cos[x]+Cos[2x]+Sin[4x]=0,x] или Cos[x]+Cos[2x]+Sin[4x]=0;
Solve[x^5+x^4+x+1=0,x] или x^5+x^4+x+1=0;
Solve[Log[3,x^2+x+1]-Log[9,x^2]=0,x] или \Log[3,x^2+x+1]-Log[9,x^2]=0.

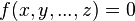Если Ваше уравнение содержит несколько переменных, то запись: f[x, y,…,z]=0 даст весьма разнообразный набор сведений, таких как решение в целых числах, частные производные функции $f$ и т. д. Чтобы получить решение уравнения вида $f(x,y,...,z)=0$ по какой-либо одной из переменных, нужно написать в строке: Solve[f[x, y, …, z]=0, j], где $j$ — интересующая Вас переменная.

Примеры

Cos[x+y]=0 или Solve[Cos[x+y]=0,x] или Solve[Cos[x+y]=0,y];
x^2+y^2-5=0 или Solve[x^2+y^2-5=0,x] или Solve[x^2+y^2-5=0,y];
x+y+z+t+p+q=9.

Решение неравенств

Решение в Wolfram Alpha неравенств типа 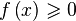$f(x)>0$ , $f\left( x \right) \geqslant 0$ полностью аналогично решению уравнения $f(x)=0$ . Нужно написать в строке WolframAlpha: f[x]>0 или f[x]>=0 или Solve[f[x]>0, x] или Solve[f[x]>=0,x].

Примеры

Cos[10x]-1/2>0 или Solve[Cos[10x]-1/2>0,x];
x^2+5x+10>=0 или Solve[x^2+5x+10>=0,x].

Если Ваше неравенство содержит несколько переменных, то запись: f[x, y,…,z]>0 или f[x, y,…,z]>=0 даст весьма разнообразный набор сведений, как и в случае соответствующих уравнений. Чтобы получить решение такого неравенства по какой-либо одной из переменных нужно написать в строке: Solve[f[x, y,…,z]>0,j] или Solve[f[x, y,…,z]>=0,j], где $j$ — интересующая Вас переменная.

Примеры

Cos[x+y]>0 или Solve[Cos[x+y]>0,x] или Solve[Cos[x+y]>0,y];
x^2+y^3-5<0 или Solve[x^2+y^3-5<0,x] или Solve[x^2+y^3-5<0,y];
x+y+z+t+p+q>=9.

Решение различных систем уравнений, неравенств и уравнений

Решение систем различного вида в Wolfram Alpha крайне просто. Достаточно набрать уравнения и неравенства Вашей системы, точно так, как это описано выше в пунктах 7. и 8., соединяя их союзом «И», который в Wolfram Alpha имеет вид &&.

Примеры

x^3+y^3==9&&x+y=1;
x+y+z+p==1&&x+y-2z+3p=2&&x+y-p=-3;
Sin[x+y]+Cos[x+y]==Sqrt[3]/4&&x+y²=1;
Log[x+5]=0&&x+y+z<1.

Построение графиков функций

Сервис Wolfram Alpha поддерживает возможность построения графиков функций как вида $f(x)$ , так и вида $f(x,y)$ . Для того, чтобы построить график функции $f(x)$ на отрезке $x \in \left[ {a,b} \right]$ нужно написать в строке Wolfram Alpha: Plot[f[x],{x, a, b}]. Если Вы хотите, чтобы диапазон изменения ординаты $y$ был конкретным, например $y \in \left[ {c,d} \right]$ , нужно ввести: Plot[f[x],{x, a, b},{y, c, d}].

Примеры

Plot[x^2+x+2, {x,-1,1}];
Plot[x^2+x+2, {x,-1,1},{y,-1,5}];
Plot[Sin[x]^x, {x,-Pi,E}];
Plot[Sin[x]^x, {x,-Pi,E},{y,0,1}].

Если Вам требуется построить сразу несколько графиков на одном рисунке, то перечислите их, используя союз «И»:Plot[f[x]&&g[x]&&h[x]&&…&&t[x],{x, a, b}].

Примеры

Plot[x&&x^2&&x^3, {x,-1,1},{y,-1,1}];
Plot[Sin[x]&&Sin[5x]&&Sin[10x]&&Sin[15x], {x,-5,5}].

Для того, чтобы построить график функции $f(x,y)$ на прямоугольнике $x \in \left[ {a,b} \right],y \in \left[ {c,d} \right]$ , нужно написать в строке Wolfram Alpha: Plot[f[x, y],{x, a, b},{y, c, d}]. К сожалению, диапазон изменения аппликаты $z$ пока что нельзя сделать конкретным. Тем не менее, интересно отметить, что при построении графика функции $f(x,y)$ Вы получите не только поверхность, которую она определяет, но и «контурную карту» поверхности (линии уровня).

Примеры

Plot[Sin[x^2+y^2],{x,-1,-0.5},{y,-2,2}];
Plot[xy,{x,-4,4},{y,-4,4}].

Математический анализ

Wolfram Alpha способен находить пределы функций, последовательностей, различные производные, определенные и неопределенные интегралы, решать дифференциальные уравнения и их системы и многое многое другое.

Пределы

Для того, чтобы найти предел последовательности 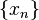$\left\{ {{x_n}} \right\}$ нужно написать в строке Wolfram Alpha: Limit[x_n, n -> Infinity].

Примеры

Limit[n^3/(n^4 + 2*n), n -> Infinity];
Limit[(1+1/n)^n, n -> Infinity].

Найти предел функции $f(x)$ при $x \to a$ можно совершенно аналогично: Limit[f[x], x -> a].

Примеры

Limit[Sin[x]/x, x -> 0];
Limit[(1-x)/(1+x), x -> −1].

Производные

Для того, чтобы найти производную функции $f(x)$ нужно написать в строке WolframAlpha: D[f[x], x]. Если Вам требуется найти производную n-го порядка, то следует написать: D[f[x], {x, n}]. В том случае, если Вам требуется найти частную производную функции $f(x,y,z,...,t)$ напишите в окне гаджета: D[f[x, y, z,…,t], j], где $j$ — интересующая Вас переменная. Если нужно найти частную производную по некоторой переменной порядка n, то следует ввести: D[f[x, y, z,…,t], {j, n}], где $j$ означает тоже, что и Выше.

Важно подчеркнуть, что Wolfram Alpha выдает пошаговое нахождение производной при нажатии на «Show Steps» в правом верхнем углу выдаваемого ей ответа.

Примеры

D[x*E^x, x];
D[x^3*E^x, {x,17}];
D[x^3*y^2*Sin[x+y], x];
D[x^3*y^2*Sin[x+y], y],
D[x/(x+y^4), {x,6}].

Интегралы

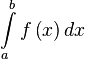Для того, чтобы найти неопределенный интеграл от функции $f(x)$ нужно написать в строке WolframAlpha: Integrate f[x], x. Найти определенный интеграл $\int\limits_a^b {f\left( x \right)dx}$ так же просто: Integrate[f[x], {x, a, b}] либо Integrate f(x), x=a..b.

Важно подчеркнуть, что Wolfram Alpha выдает пошаговое нахождение интеграла при нажатии на «Show Steps» в правом верхнем углу выдаваемого ей ответа.

Примеры

Integrate[Sin[x]/x², x];
Integrate[x^10*ArcSin[x], x];
Integrate[(x+Sin[x])/x, {x,1,100}];
Integrate[Log[x^3+1]/x^5, {x,1,Infinity}].

Дифференциальные уравнения и их системы

Чтобы найти общее решение дифференциального уравнения $F(x,y,y^{/},y^{//},...,y^{(n)}) = 0$ нужно написать в строке WolframAlpha: F[x, y, y',y'',…] (при k-й производной y ставится k штрихов).

Если Вам требуется решить задачу Коши, то впишите: F[x, y, y',y'',…], y[s]==A,y'[s]==B, …. Если нужно получить решение краевой задачи, что краевые условия, так же перечисляются через запятую, причем они должны иметь вид y[s]==S.

Решение систем дифференциальных уравнений также просто, достаточно вписать: {f_1,f_2,…,f_n}, где f_1, f_2, …, f_n — дифференциальные уравнения, входящие в систему. К сожалению, решение задач Коши и краевых задач для систем дифференциальных уравнений пока-что не поддерживается.

Примеры

y'''+y''+y=Sin[x];
y''+y'+y=ArcSin[x];
y''+y+y^2=0;
y''=y, y[0]==0, y'[0]=4;
y+x*y'=x, y[6]=2;
y'''[x]+2y''[x]-3y'[x]+y=x, y[0]=1, y[1]=2, y'[1]=2;
{x'+y'=2, x'-2y'=4}.

Ошибки при работе с системой

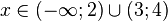Система может допускать некоторые ошибки при решении сложных задач. К примеру, если попытаться решить неравенство $\frac{3x^2-18x+24}{2x-2}-\frac{3x-12}{2x^2-6x+4}<0$ , для чего ввести запрос solve (3x^2-18x+24)/(2x-2)-(3x-12)/(2x^2-6x+4)<0, то Wolfram|Alpha выдаст в качестве ответа промежуток $x \in (-\mathcal {1}; 2) \cup (3; 4)$ , в котором будет присутствовать точка 1, обращающая оба знаменателя исходного неравенства в 0. Так что весь риск и вся ответственность при использовании Wolfram|Alpha ложится на Вас. Скорее всего, данные недочеты будут скоро исправлены.

Разложение на множители

Например, разложить на множители

x²/3 - 3x + 12

Запишем как

factor x^2/3 - 3x + 12

и нажимаем равно (=).

Например, разложить на слагаемые

Запишем как

Partial fraction expansion(1-x^2)/(x^3+x)

используются формулы разложения функций в ряд Тейлора (Taylor series) и ряд Маклорена (Maclaurin series) или

Series expansion at x=0

Разложить в ряд Лорана:

Laurent expansion z*cos(1/z) at z =0

Чтобы упростить выражение f[x], наберите команду Simplify[f[x]]

Комплексно сопряженное z*

Египетская дробь:

Egyptian fraction expansion:

11/30=1/3+1/30

parametric plot (3*cos t, sin t, 2t), t=0..2pi

interpolation polynomial {1,4,9,16}

Транспонировать матрицу: transpose {{8,2,-3,2},{-6,3,-2,1},{3,8,4,-8},{2,1,-6,2}}

Обратная матрица inverse {{a, b}, {c, d}}

Собственные числа (вектора) матрицы: eigenvalues( ( transpose{{1,0,0,0},{0,1,0,0},{0,0,1,0},{0,0,0,1}})-1/67.42598*({{8,2,-3,2},{-6,3,-2,1},{3,8,4,-8},{2,1,-6,2}}*{{8,2,-3,2},{-6,3,-2,1},{3,8,4,-8},{2,1,-6,2}}))

Решение СЛАУ : {{8,2,-3,2},{-6,3,-2,1},{3,8,4,-8},{2,1,-6,2}}*{{x_1},{x_2},{x_3},{x_4}}={{102},{-47},{-122},{-24}}

{{-9,5,2},{5,-6,3},{4,1,-5}}*{{x},{y},{z}}={{0},{0},{0}}

Интегральное преобразование Лапласа ---- LT

Обратное преобразование Лапласа -- ILT