Критерии согласия
Для проверки соответствия эмпирического распределения теоретическому (гипотезы) можно наложить на гистограмму теоретическую кривую (рис. 6).
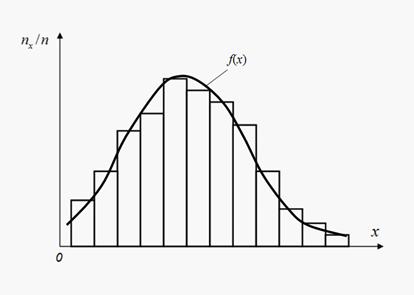
Рис. 6. Гистограмма и теоретическая плотность распределения
При этом неизбежно обнаружатся расхождения, либо случайные, связанные с ограниченным объемом наблюдений, либо свидетельствующие о неправильном подборе выравнивающей функции (гипотезы). Для ответа на этот вопрос используют так называемые «критерии согласия». Для этого вводится случайная величина U, характеризующая расхождение эмпирического и теоретического распределений в предположении истинности теоретического распределения. Мера расхождения U выбирается таким образом, чтобы функция ее распределения 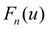 не зависела от вида выравниваемого (эмпирического) распределения и достаточно быстро сходилась по числу наблюдений n к предельной функции не зависела от вида выравниваемого (эмпирического) распределения и достаточно быстро сходилась по числу наблюдений n к предельной функции 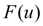 . Затем определяется фактическая степень расхождения u и оценивается вероятность . Затем определяется фактическая степень расхождения u и оценивается вероятность 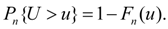 Малая величина Малая величина 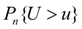 говорит о том, что полученное расхождение u в силу чисто случайных причин маловероятно, и теоретическое распределение плохо согласуется с эмпирическим. Однако, большие вероятности не могут считаться исчерпывающим доказательством истинности теоретического закона распределения и свидетельствуют лишь об отсутствии оснований его отвергнуть. говорит о том, что полученное расхождение u в силу чисто случайных причин маловероятно, и теоретическое распределение плохо согласуется с эмпирическим. Однако, большие вероятности не могут считаться исчерпывающим доказательством истинности теоретического закона распределения и свидетельствуют лишь об отсутствии оснований его отвергнуть.
Иногда поступают иначе: заранее рассчитывают меру расхождения 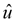 , которая может быть превышена с указанной малой вероятностью, и при , которая может быть превышена с указанной малой вероятностью, и при 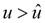 рассматриваемое теоретическое распределение отвергают. рассматриваемое теоретическое распределение отвергают.
Существует множество критериев согласия, среди которых наиболее употребительными являются критерий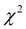 Пирсона и критерий Колмогорова-Смирнова. Пирсона и критерий Колмогорова-Смирнова.
В критерии согласия 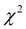 Пирсона мерой расхождения теоретического и эмпирического распределений является взвешенная сумма квадратов отклонений Пирсона мерой расхождения теоретического и эмпирического распределений является взвешенная сумма квадратов отклонений
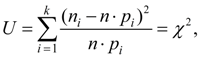 (27) (27)
где k – число интервалов разбиения значений случайной величины, 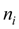 – количество наблюдений, попавшее в i-й интервал, – количество наблюдений, попавшее в i-й интервал, 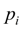 – теоретическая вероятность появления значения из i-го интервала, n – общее число наблюдений. – теоретическая вероятность появления значения из i-го интервала, n – общее число наблюдений.
В практических задачах рекомендуется иметь в каждом интервале разбиения не менее 5-10 наблюдений [3].
Обозначим через t число независимых связей, наложенных на вероятности 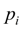 . Их общее число равно количеству характеристик теоретического распределения, подбираемых по опытным данным, плюс единица (условие нормировки . Их общее число равно количеству характеристик теоретического распределения, подбираемых по опытным данным, плюс единица (условие нормировки 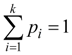 ). Таким образом, схема применения критерия ). Таким образом, схема применения критерия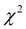 к оценке согласованности теоретического и эмпирического распределений сводится к следующему: к оценке согласованности теоретического и эмпирического распределений сводится к следующему:
1) Определяется мера расхождения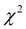 по формуле (27). по формуле (27).
2) Определяется число степеней свободы r = k – t.
3) По r и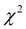 с помощью специальной таблицы [3] определяется вероятность того, что величина, имеющая распределение с помощью специальной таблицы [3] определяется вероятность того, что величина, имеющая распределение 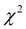 с r степенями свободы, превзойдет данное значение с r степенями свободы, превзойдет данное значение 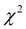 . Если эта вероятность весьма мала, гипотеза (теоретическая кривая) отбрасывается как неправдоподобная. Если же эта вероятность относительно велика, гипотезу можно признать не противоречащей полученным экспериментальным данным. . Если эта вероятность весьма мала, гипотеза (теоретическая кривая) отбрасывается как неправдоподобная. Если же эта вероятность относительно велика, гипотезу можно признать не противоречащей полученным экспериментальным данным.
Насколько мала должна быть вероятность р для того, чтобы отбросить или пересмотреть гипотезу, не решается на основе математических соображений и выкладок. На практике, если оказывается, что р < 0.1, рекомендуется проверить или повторить эксперимент. Если заметные расхождения появятся снова, следует искать другой, более подходящий для описания опытных данных закон распределения. Если же вероятность p > 0.1 (относительно велика), то это еще не может считаться доказательством справедливости гипотезы, а говорит лишь о том, что гипотеза не противоречит экспериментальным данным.
Онлайн сервис: решение задач по статистике
|

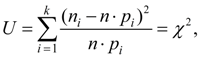 (27)
(27)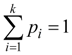 ). Таким образом, схема применения критерия
). Таким образом, схема применения критерия